Slime Mold Oracle

Fuligo septica in my back yard

Physarum polycephalum close up

The temperate rainforest around our Whaletown, British Columbia field station is home to a common slime mould Fuligo septica – otherwise known as  ‘Dog Vomit’ which is in my opinion a rather off-putting name for a very engaging life form.

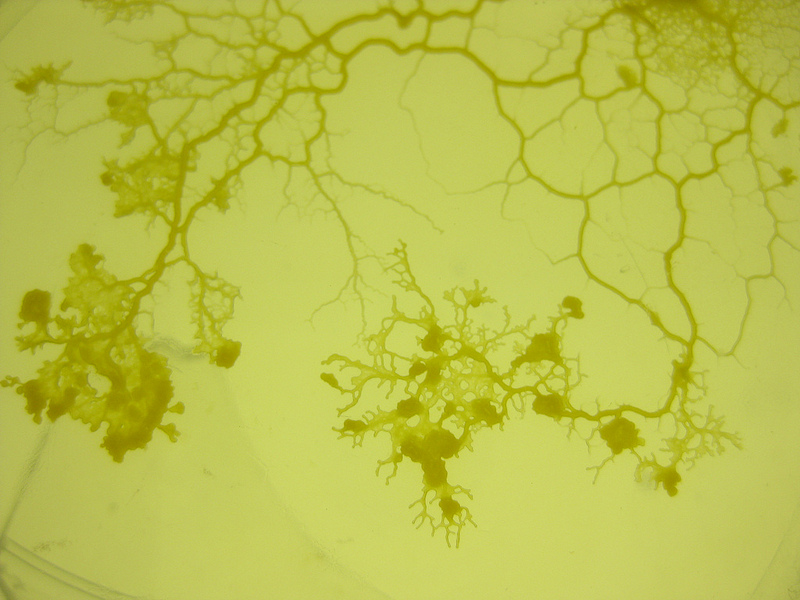
Far from being vomit or mold, these slimy masses are actually swarms of social amoebae that have combined their protoplasm and nuclei into a single super-organism called a plasmodium. Once formed, the plasmodium creeps along the forest floor until it reaches a tree stump or log, which it then climbs to so that it can release spores into slightly more active air. These then drift, settle, and eventually germinate into another generation tiny amoebas, which will one day seek each other out, join together and then start their complicated, en-masse migration process again.

This is all very fascinating, but the reason slime moulds have been the subject of such intensive research lately is that the plasmodial masses show an uncanny ability to solve complex computational problems - which is all the more remarkable given that the amoebae that constitute it have neither brain nor nervous system and are about as rudimentary a life form as you can get.

But when large numbers of these simple beings are networked into a swarm, the principle of emergence takes over which begets a unified intelligence. 

The rules governing emergence are fairly simple - as long as each constituent individual is aware and able to exchange basic sensory information with its neighbours, stimuli can be transmitted throughout the entire system, allowing it to react as a sentient whole, flowing, for example, toward attractants or away from dangers such as dehydration. This simple yet powerful mechanism is behind the flocking of birds, the movement of vehicular traffic and the evolution of memes on the internet. It is a non-hierarchical, ‘ur’-intelligence, an organizing tendency imbued in the very vibrancy of matter itself.

The lab rat of the slime mould world is the easy-to-raise species Physarum polycephalum and as such it has been the subject of much experimentation.  Lured by oatmeal flakes, Physarum can outperform robots in solving mazes and it will figure out mathematically complex problems such as how to most efficiently connect an arrangement of arbitrary points, making it astonishingly good at designing highway networks and other 'mesh' systems.  Though clearly brainless, Physarum has a rudimentary spatial memory, recognizing where it has been by sensing the slime trails it has previously left behind and focusing its foraging energy on covering new ground.

Inspired by my time hanging around with the bio-geeks at Brooklyn’s GENSPACE, I decided to put old Physarum to the test by giving it some problems I thought worthy of its impressive powers:

Physarum navigating a model IKEA store

1) The IKEA vexation:

For years I have been irked by IKEA stores. What is the most efficient way to navigate through one of them? I find IKEA to be especially frustrating and always have had trouble finding my way toward the exit without being overcome by an anxious 'trapped' feeling. For me, IKEA is prime habitat for what it called the Gruen transfer - a deliberate architectural strategy aimed at disorienting people in shopping malls; an invocation of spatial confusion that makes us lose track of our original intentions and buy stuff we don’t need. I wondered if the slime mould could resist such distractions and efficiently find its way through an IKEA without getting sidetracked? To put this to the test, I built a tiny petri-dish sized model of the floor plan of the IKEA, modelled on the store in Richmond, British Columbia, which is more or less typical. Each department was baited with an oatmeal flake and I plunked a little bit of Physarum culture down near the store's entrance to see what it could do.

slime mold says ‘yes!’

second choice hazy

at the moment of ‘yes or no?’

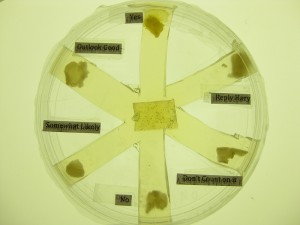
2) The Future is out there: Decisions involving the future are hard for me to make, especially if there are a lot of equal seeming options. Throughout history, we’ve consulted soothsayers, fortune tellers and ouija boards in hopes we might get some guidance on how to choose between those many forks we encounter in life’s road.  I’ve often despair and then make a seemingly random choice. If slime moulds are so good at solving problems in the here and now, how might they do in sussing out what hasn’t yet happened? Could they help me ‘Magic 8-Ball’ style make decisions on what to do next?  Well, I was a little too clumsy to build a proper ‘8-Ball’, but I managed to make a reasonably convincing ‘6-Ball’ simulacrum, by cutting six (approximately identical) radial paths into the agar of a petri dish and having the slime mould choose which one it wanted to go down. I baited  each ‘choice’ with a flake of oatmeal and labelled them: ‘yes,’ ‘no,’ ‘outlook good,’ ‘reply hazy,’ ‘somewhat likely,’ and ‘don’t count on it!’ I’d ask the slime mould a (secret) question then wait a few hours to see what it decided. Well those of you who have had scientific training are probably about to bust a blood vessel about now, but bear with me!

ballistic behaviour

Perhaps predictably, the IKEA ‘maze’ problem was quickly solved by Physarum. It relentlessly streamed from one ‘department’ to the next in search of its oatmeal rewards and within a couple of days, it arrived at the exit hungry for more. This is a very basic slime mould-solvable problem. Physarum tends to behave in what is called a ‘ballistic’ manner; once they have sensed a stimulus they will try to flow toward it taking the most direct route possible. Except when they don't Because unlike a non-sentient being, slime mould will often abort its migration toward an attractant, if it senses a rival has gotten there first. Sometimes though, competitors will merge into one happy super organism and share the the love and the bounty.

inputs A and B seeking oatmeal

A and B combining to one output

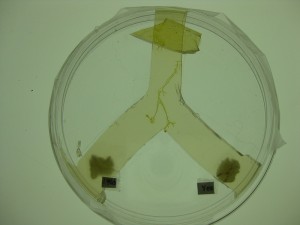
This makes for some interesting possibilities for ‘non-digital’ logic. Let's say we place slime moulds, (let’s call them ‘A’ and ‘B’) in each of the two forks of a ‘Y’ shaped path and put an oatmeal flake in the remaining leg. If the slime moulds were to behave consistently - that is to say ‘digitally’, you would have the basis for what is called an Exclusive ‘OR’ gate, a common component of computer logic.

There has been some research done on this by Andrew Adamatzky at the University of the West of England. Given the slime moulds’ usual aversion to the presence of a rival, the one that gets to the bait first will dissuade the other. So in logic gate terms the presence of 'A' or 'B' (the inputs) will generate an output, i.e. either 'A' or 'B' gets to the oatmeal.

‘A’ and ‘B’ can’t both reach the oatmeal because the presence of one will (most of the time) repel the other, so the gate is considered ‘exclusive.’ But because slime moulds, though simple, are living things with their own agency, they don’t always do what we expect.

When ‘A’ and ‘B’  break convention and flow together to share the oatmeal, the logic gate becomes ‘non-exclusive,’ i.e input ‘A’ or ‘B’ or both can appear as outputs.

Sometimes even that doesn't happen and a slime mould gets distracted and decides to loiter around the perimeter of the petri dish, boycotting the experiment altogether, despite the presence of tasty oatmeal.

Who knows why? Are they following their bliss? Or are they just confused?

To my mind, these exceptions to behaviour we deem 'logical' are the most interesting results. If we develop a new class of biological computers based on slime mold logic, the outputs generated might have a charming and useful variability. This might more closely emulate the real world ‘twitchiness’ of such social  phenomena as how we behave in markets (i.e. we don't always act rationally or in our own self interest despite what economists would like us to do), or how other conglomorations such as riots or election results, which are also less than rational processes.

this time- both outputs are generated!

And as for predicting my future, my slime mold oracle was initially quite decisive.  It answered my first (secret) question with a resounding 'Yes,'  but then started creeping around to check out other potential possibilities. If this was doubt then that to me seems perfectly reasonable!